Fundamental Review of the Trading Book

The Fundamental Review of the Trading Book (FRTB) is an international standard developed by the Basel Committee on Banking Supervision (BCBS), which determines the amount of capital that banks must hold against market risk.

The primary objective of FRTB is to address the shortcomings revealed during the 2007–2008 global financial crisis and to ensure that banks measure their market risks more accurately and consistently. In this context, FRTB adopts the following key goals:

Clarifying the boundary between the trading book and the banking book: FRTB aims to clearly distinguish between assets held for trading purposes and those intended to be held to maturity. This helps to prevent regulatory capital arbitrage between the two books.
Introducing stricter measures against market illiquidity risk: The framework encourages banks to consider market liquidity constraints and their implications for capital adequacy, promoting more prudent risk management during periods of low liquidity.
Changing the risk measurement approach: FRTB replaces the traditional Value at Risk (VaR) metric with Expected Shortfall (ES) for measuring risk under stress conditions. Unlike VaR, Expected Shortfall captures both the magnitude and likelihood of tail risk events, providing a more realistic assessment of risk during extreme market volatility. This makes ES a more appropriate metric for determining regulatory capital requirements.
Restructuring the internal models approach (IMA): In response to weaknesses observed during the global financial crisis, the internal models framework has been comprehensively redesigned. The approval and supervisory processes for using internal models have been significantly strengthened, establishing tighter controls over model risk. Additionally, sensitivity-based standard approaches have been introduced to better reflect actual market risk exposures.

Under the FRTB framework, two primary approaches are provided for the calculation of market risk: the Standardised Approach (SA) and the Internal Models Approach (IMA).

·Standardised Approach (SA): Under this approach, banks calculate the sensitivities to standardized risk factors and incorporate default risk and residual risk into the calculations. The Standardised Approach offers a more transparent and supervisory-friendly structure, making it easier for regulators to monitor and evaluate.

·Internal Models Approach (IMA): Banks may calculate market risk capital requirements based on their internally developed models. However, this approach is only available to institutions that meet specific minimum requirements and obtain approval from their national supervisory authority.

In the following sections, we will provide a detailed explanation of the Standardised Approach, its components, and walk through sample calculations. The Standardised Approach (SA) consists of three main components:

Sensitivities-Based Method (SBM): This method requires banks to calculate the sensitivities (delta, vega, and curvature) of trading book instruments to specific risk factors. These sensitivities are grouped under seven major risk classes: interest rate, equity, foreign exchange, commodity, and credit spread risk (both non-securitisation and securitisation). Each sensitivity is converted into a capital requirement using prescribed risk weights and correlation matrices.
Default Risk Charge (DRC): The DRC covers potential jump-to-default losses that may occur if the issuer of a financial instrument defaults. This calculation is performed separately for each instrument and is based on factors such as notional amount, market value, and probability of default.
Residual Risk Add-On (RRAO): The RRAO accounts for complex and hard-to-model risks not captured by SBM or DRC, such as risks associated with structured products. This component is calculated by applying fixed risk weights to specific types of instruments.

The sum of these three components constitutes the minimum capital requirement that a bank must hold under the Standardized Approach. This structure enables banks to assess their market risks in a more granular and comprehensive manner.

Sensitivities-Based Method – SBM:

In the calculation of capital requirements, predefined risk factors are used to determine the delta, vega, and curvature sensitivities of financial instruments. Once the risk-weighted sensitivities are calculated, exposures within the same bucket and risk class are aggregated. These steps are detailed in MAR21.8 to MAR21.14.

The regulation defines seven distinct risk classes to be used in market risk calculations (MAR21, paragraph 21.1):

General Interest Rate Risk (GIRR): Reflects the change in the price of a financial instrument due to movements in interest rates.
Credit Spread Risk – Non-Securitisation (CSR): Measures the impact of changes in credit spreads on the value of non-securitised instruments.
Credit Spread Risk – Securitisation Non-Correlation Trading Portfolio (CSR Non-CTP): Refers to securitised products exposed to credit spread risk without correlation features.
- Examples: Asset-Backed Securities (ABS), Mortgage-Backed Securities (MBS), Covered Bonds.
Credit Spread Risk – Correlation Trading Portfolio (CSR CTP): Applies to securitised instruments with correlation structures or arbitrage features.
- Examples: Collateralised Debt Obligations (CDOs), tranche CDSs, nth-to-default baskets.
Equity Risk: Sensitivity to changes in equity prices.
Commodity Risk: Sensitivity to commodity price movements.
Foreign Exchange (FX) Risk: Sensitivity to exchange rate fluctuations.

Sensitivity analyses are calculated for the defined risk classes based on specified risk factors. These analyses include delta, vega, and curvature sensitivity calculations.

PV01 (Present Value of a 1 basis point), is traditionally defined as the change in the value of a financial instrument resulting from a 1 basis point (0.01%) change in the underlying rate. Under FRTB, PV01 is interpreted as the sensitivity of the instrument’s value to a shift in a specified risk factor.

Sensitivity analyses are calculated for the defined risk classes based on specified risk factors. These analyses include delta, vega, and curvature sensitivity calculations.

PV01 (Present Value of a 1 basis point), is traditionally defined as the change in the value of a financial instrument resulting from a 1 basis point (0.01%) change in the underlying rate. Under FRTB, PV01 is interpreted as the sensitivity of the instrument’s value to a shift in a specified risk factor.

The calculation of sensitivity or PV01 is performed by applying a 1 basis point shift in the risk-free yield curve at a specific tenor (maturity point). The general formulation of the calculation is provided in MAR21, paragraph 21.42.Sensitivity analyses are calculated for the defined risk classes based on specified risk factors. These analyses include delta, vega, and curvature sensitivity calculations.

The calculation of sensitivity or PV01 is performed by applying a 1 basis point shift in the risk-free yield curve at a specific tenor (maturity point). The general formulation of the calculation is provided in MAR21, paragraph 21.42. MAR21, paragraph 21.42.

The risk-free yield curve used for delta calculations should be based on instruments with minimal credit risk, such as Overnight Index Swaps (OIS). The tenors of the yield curve—0.25 year, 0.5 year, 1 year, 2 years, 3 years, 5 years, 10 years, 15 years, 20 years, and 30 years—are defined as delta risk factors under the framework. (MAR21, paragraph 21.8)

Risk factors are grouped into buckets based on currency. For each bucket, risk weights are prescribed by the regulator.

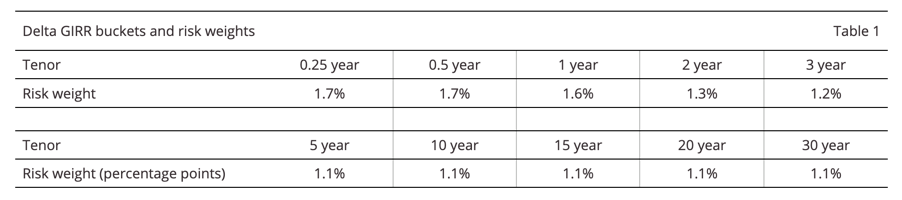
For currencies defined by the Basel Committee—EUR, USD, GBP, AUD, JPY, SEK, and CAD—the square root of the risk weights must be used for reporting purposes. (MAR21, paragraph 21.44)

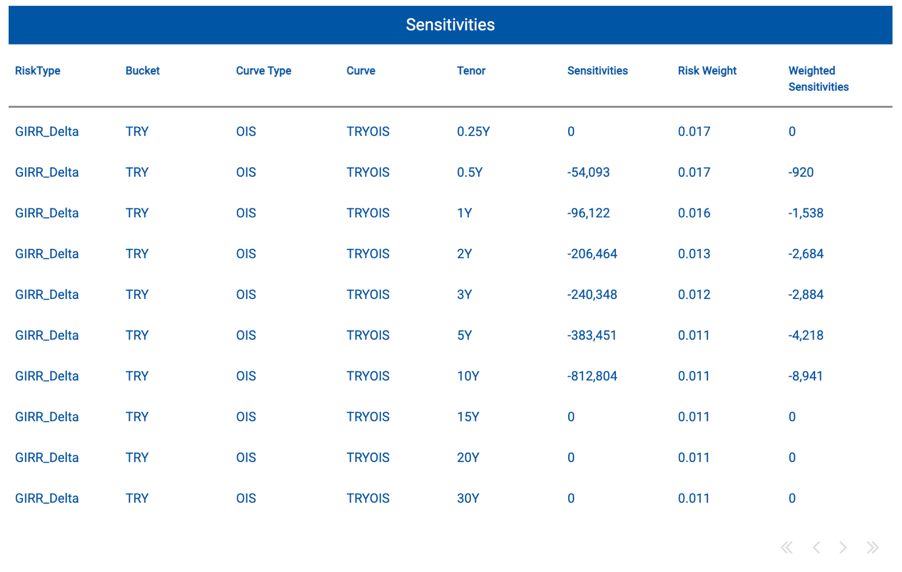
The weighted sensitivities for each bucket are calculated by multiplying the sensitivity values by the corresponding risk weights assigned to the bucket. (MAR21, paragraph 21.4)

_{Sensitivity analysis calculated using the key rate duration method with Rhoova}

The weighted risk sensitivities, combined with the correlations between risk factors, are used to calculate the bucket-level capital requirement according to the following formula:

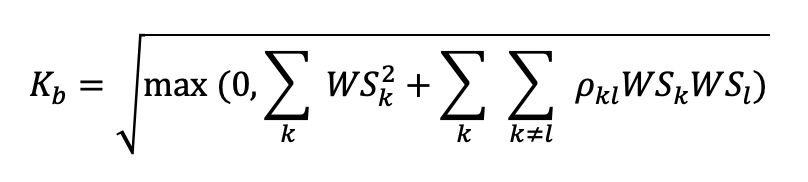
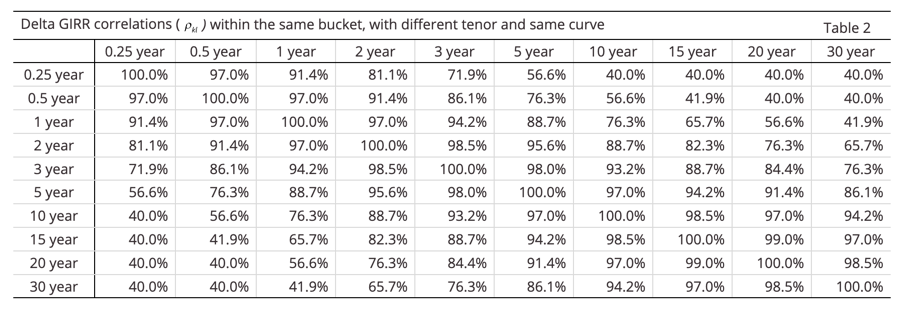
The correlation matrix between risk factors as prescribed by the regulator is as follows:

Correlation Scenarios Calculated with Rhoova:

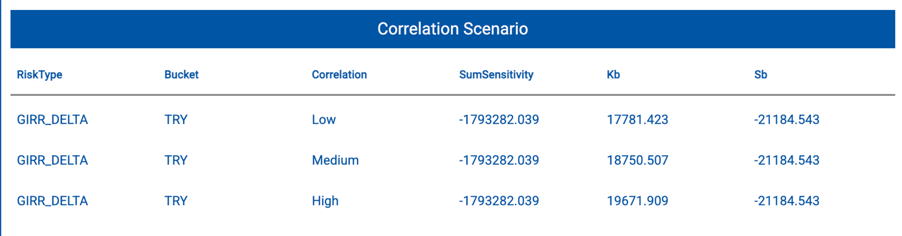
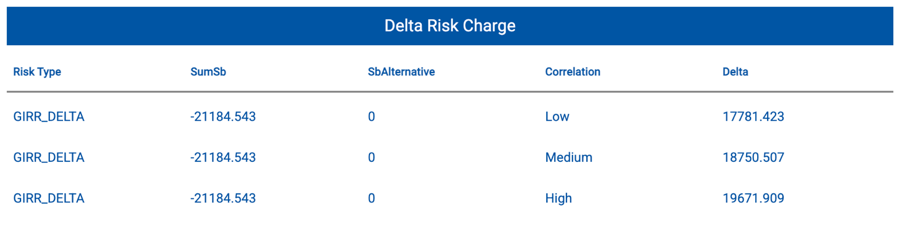
After the bucket-level capital requirement is calculated, the inter-bucket diversification risk is assessed using three different correlation scenarios. Based on these scenarios, the final capital requirement is determined by selecting the most conservative (i.e., highest) result among them.

FRTB delta calculations can be performed through Rhoova. Rhoova enables sensitivity analysis in two distinct ways. First, by computing key rate durations based on the tenors of the risk factors as defined by the regulator. Second, by evaluating the impact of rate shifts individually at each tenor to capture sensitivities across the curve. This method allows for the calculation of delta sensitivities for each maturity bucket, aligned with the regulatory requirements of the Standardised Approach (SA) under FRTB.(https://github.com/rhoova/rhoova-examples/blob/main/python_examples/Portfolio/FRTB/SensitivityCalculation.ipynb)

The other calculation method is based on the RiskMetrics approach, where cash flows are distributed across the given maturity buckets. Although the total PV01 values are generally similar in both methods, the key rate duration method is more suitable for FRTB, as it distributes floating rate exposures across all relevant tenors.(https://www.msci.com/documents/10199/5915b101-4206-4ba0-aee2-3449d5c7e95a sayfa 117)

Curvature risk, also known as non-linear risk, refers to the non-linear response of an asset’s value to large market movements. Since delta risk does not capture the impact of such significant shifts, curvature risk has been introduced as an additional component in capital calculations under FRTB.

Curvature risk is calculated by applying upward and downward parallel shocks across all tenors of the yield curve. (MAR21, paragraph 21.5)

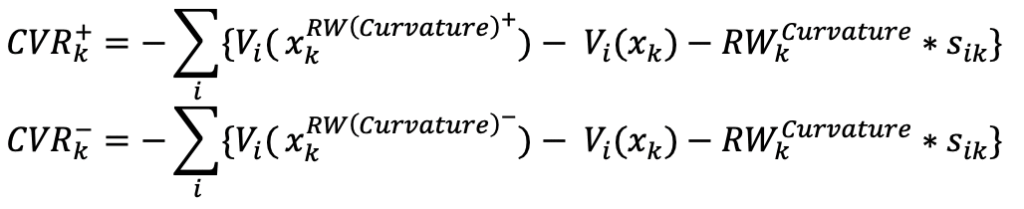
When calculating curvature risk, the risk weight used is the highest risk weight across all tenors within the relevant risk class. (MAR21, paragraph 21.99)

After applying upward and downward shocks, the capital requirement (Kb) is calculated using inter-bucket correlations.

In the calculation of inter-product and inter-bucket correlations, for the high correlation scenario, the prescribed correlation values are multiplied by 1.25, but capped so that they do not exceed 1.

For the low correlation scenario, the calculation is performed as follows:

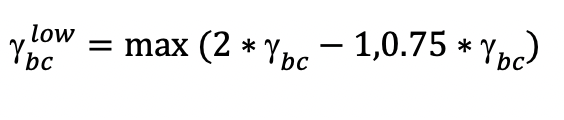
Vega, like delta, is a linear risk measure and is defined as the sensitivity of an asset’s price to changes in volatility. Under FRTB, it is used to determine the capital requirement for options and option-sensitive instruments in response to changes in implied volatility. The capital requirement for vega risk is calculated similarly to delta, involving the application of prescribed risk weights and correlation structures to the volatility sensitivities across defined risk classes and buckets.

Links:

https://www.bis.org/basel_framework/chapter/MAR/21.htm

https://demo-rhoova.anvil.app

https://github.com/rhoova/rhoova-examples/tree/main/python_examples/Portfolio/FRTB